알고리즘 합병정렬(Merge sort) 그림으로 쉽게 이해하기
안녕하세요.
로스윗의 코딩캠프입니다.
오늘은 알고리즘 정렬 중에서
합병정렬(Merge sort)에 대한 포스팅을 진행하겠습니다.
정말 어렵지 않으니 잘 따라와주세요.
- 합병정렬(머지소트, Merge sort)
이번 포스팅에서는 합병정렬(머지소트, Merge sort)에 대해서 알아보도록 하겠습니다.
합병정렬(Merge sort)과 다음 포스팅에서 다룰 퀵정렬(Quick sort)이 정렬 알고리즘의 핵심이라고 보시면 될 것 같습니다.
그래서 여기서 부터는 이전에 배웠던 삽입정렬, 버블정렬의 방식과는 다르게
조금 더 복잡한 형태로 정렬을 진행하게 됩니다.
1. 합병정렬(머지소트, Merge sort) 이란?
합병정렬(Merge sort)은
1. 하나의 리스트를 두개의 균등한 크기로 분할을 하고,
2. 분할된 부분 리스트들을 정렬을 한 다음에,
3. 정렬된 부분 리스트들을 하나로 합치면서 전체가 정렬된 리스트가 되게 하는 방법입니다.
2. 합병정렬(머지소트, Merge sort) 그림으로 쉽게 이해하기
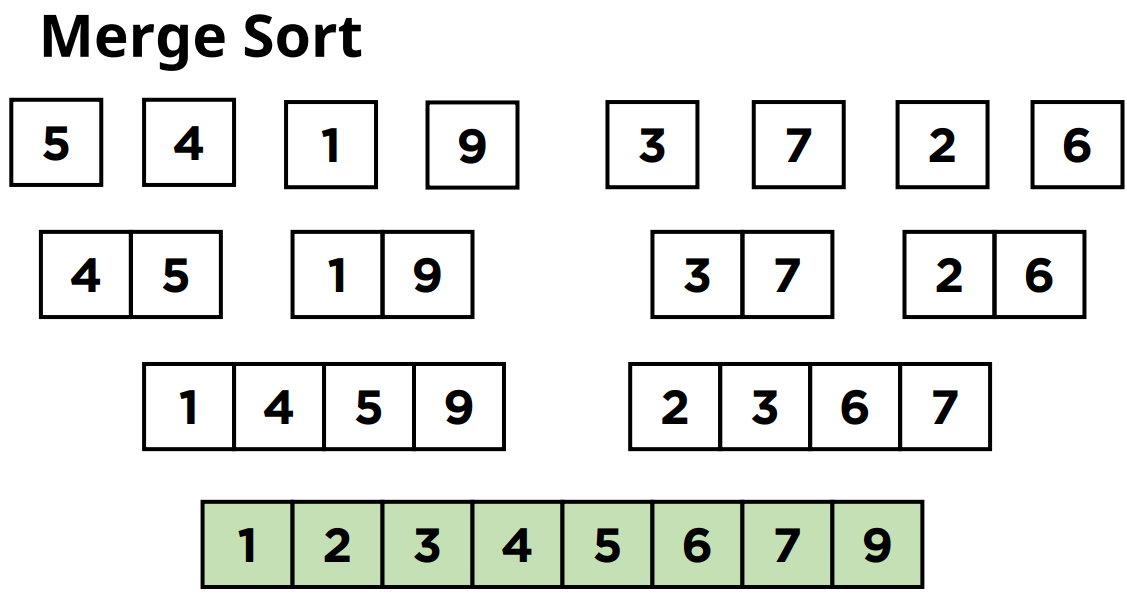
이렇게 아래의 그림과 같은 하나의 전체 리스트가 주어진 상황이라고 가정을 해보겠습니다.
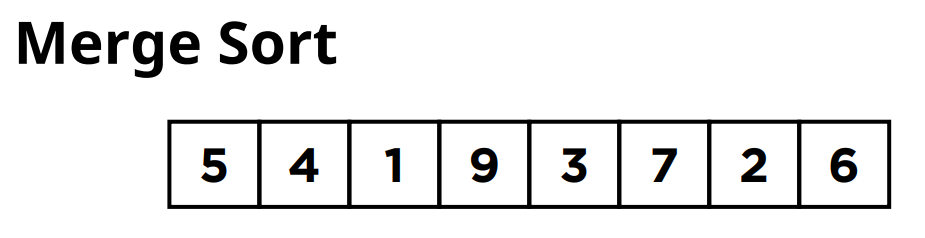
먼저 이 리스트를 크기가 같은 두개의 부분 리스트로 분할을 합니다.
그러면은 여기서는 크기가 4인 서브 리스트 2개를 만들 수 있겠죠.
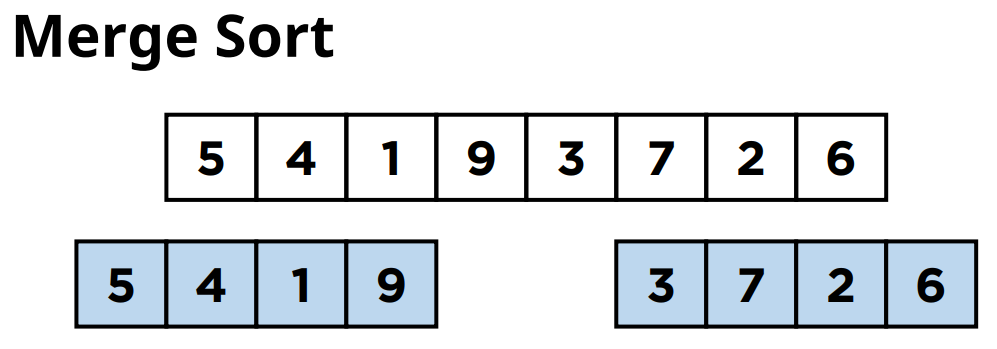
여기서 이 서브 리스트들을 또 같은 크기의 부분 리스트들로 크기를 분할해줍니다.
그러면 크기가 2인 부분 리스트 4개가 나오게 되겠죠.

이 분할을 언제까지 해야 하냐면 부분 리스트의 사이즈가 1이 될때까지 분할을 해줘야합니다.
그래서 한 번 더 같은 크기의 리스트로 분할을 하면 이제 크기가 1인 서브리스트 8개가 나오게 됩니다.
그리고 서브리스트의 크기가 1이 되었기 때문에 분할이 종료가 됩니다.
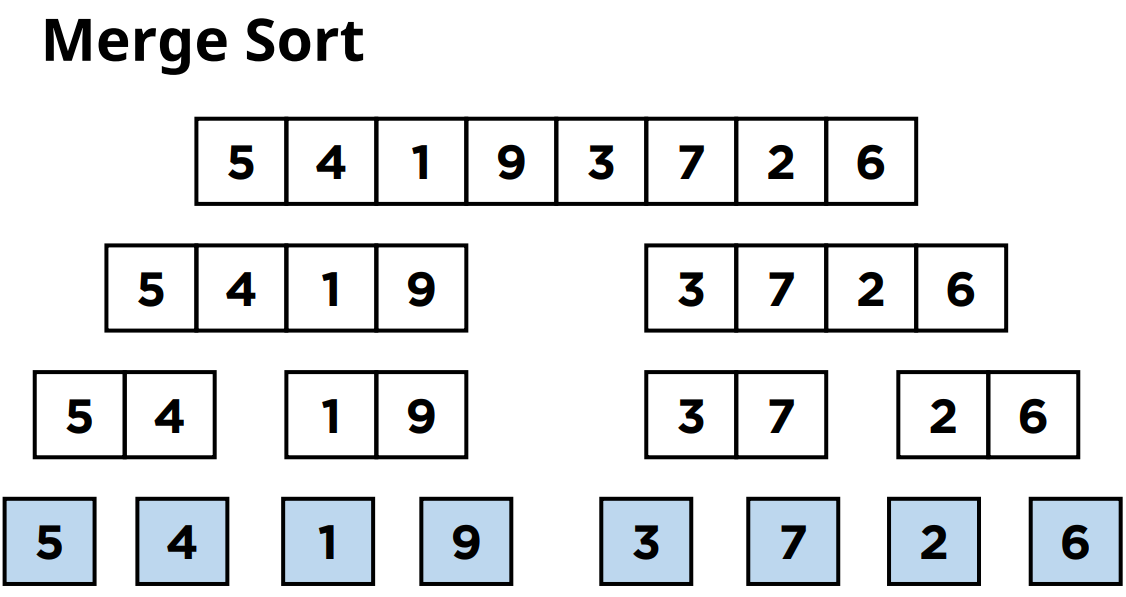
그러면 이제부터 크기가 1인 분할된 부분리스트들을 합치면서 정렬을 시작하게 됩니다.
분할된 부분리스트들을 정렬을 할 때는 한번에 정렬하는게 아니라
분할과 동일한 크기로 부분 리스트들을 합쳐나가게 됩니다.
그래서 크기가 1인 8개의 서브리스트들을 크기가 2인 리스트 4개로 합치는 것부터 시작을 하게 됩니다.
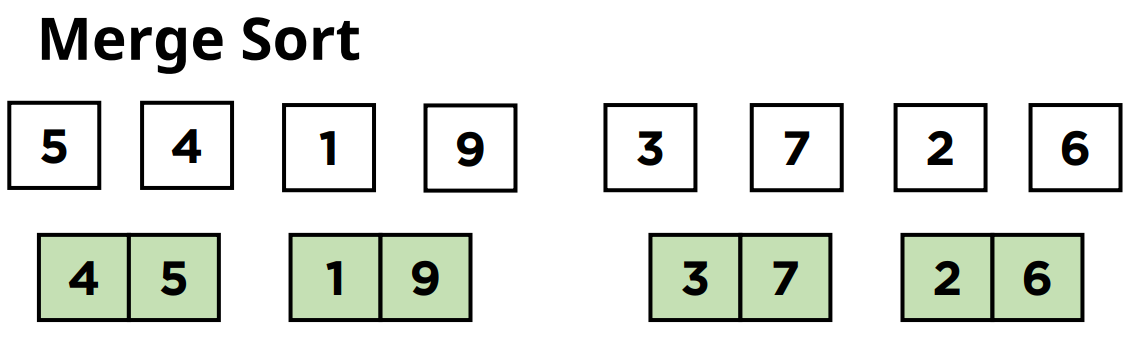
합치면서 각 원소들은 자신의 위치에 정렬되기 때문에 합쳐진 서브 배열들은 정렬된 상태를 유지하게 됩니다.
그래서 5와 4는 정렬을 해서 4와 5의 순서로 정렬이 되고 나머지도 정렬된 순서를 유지하면서 배열이 합쳐지게 됩니다.
그 다음으로 크기가 2인 서브 리스트들을 합쳐서 크기가 4인 서브리스트 2개로 만들어 줍니다.
그래서 4, 5 / 1, 9 이 2개의 서브리스트는 합쳐지면서 1, 4, 5, 9의 순서로 정렬이 되고
3, 7 / 2, 6 이 2개의 서브리스트는 합쳐지면서 2, 3, 6, 7의 순서로 정렬이 됩니다.

이 합치는 과정을 원래 크기의 배열이 될 때까지 반복하는거에요.
그래서 이제는 여기서 한 번만 더 하면 되겠죠.
그래서 마지막으로 합치는 과정에서 크기가 8인 정렬된 배열을 얻을 수 있게 됩니다.
3. 분할정복(Divide and conquer)알고리즘
이렇게 하나의 문제를 동일한 유형의 작은 문제들로 분할한 다음에
작은 문제에 대한 결과를 조합해서 큰 문제를 해결하는 방식의 알고리즘을
분할정복(Divide and conquer)알고리즘이라고 합니다.
분할정복은 알고리즘 풀이 기법에 있어서 적지 않게 쓰이는 패턴입니다.
또 분할 정복 알고리즘은 보통 재귀 함수로 구현된다는 특징이 있습니다.
그래서 합병정렬(merge sort)도 재귀함수를 통해서 구현을 하게 될 것입니다.
4. 합병정렬 시간복잡도 증명
합병정렬(merge sort)의 시간복잡도는 O(NlogN)입니다.
그 이유는 분할과정에 있습니다.
분할 과정은 한 번 시행할 때마다 리스트의 크기가 1/2씩 감소를 하게 되죠.
그래서 처음 N개의 요소(element)에서 한 번 분할을 하게 되면 n/2개의 리스트 2개를 얻게 됩니다.
그 상태에서 또 분할을 수행하게 되면 n/4 크기의 서브리스트 4개를 얻게 됩니다.
이런 분할 연산은 배열의 크기가 1이 될 때까지 반복해야 하는데,
리스트의 크기가 2라면 이 분할은 한 번, 그리고 4개라면 2번,
그리고 리스트의 개수가 총 8개라면 3번을 반복해야 크기가 1인 부분리스트들을 얻을 수 있어요.
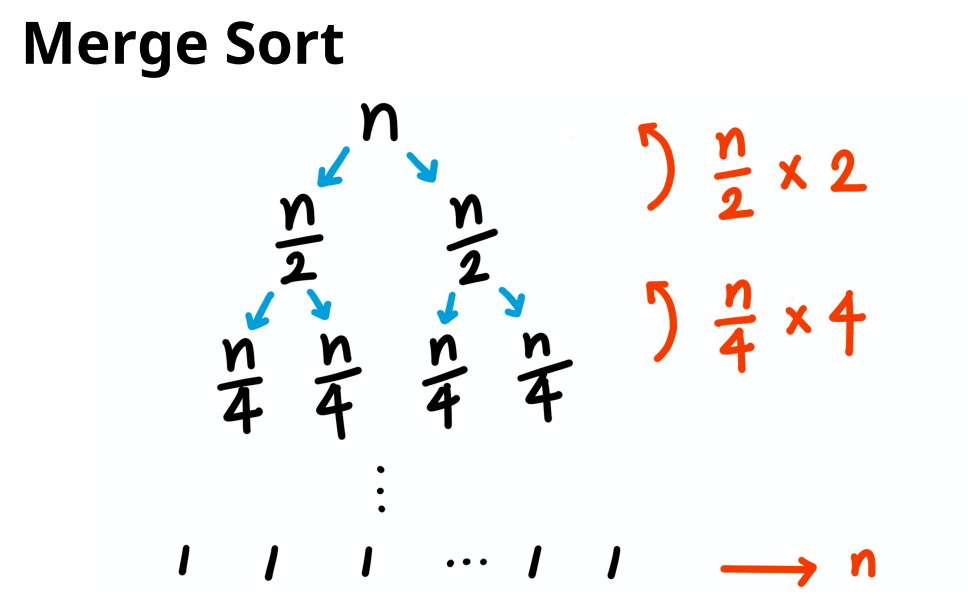
즉, N개의 요소(element)가 있는 상황에서
N이 2의 K제곱이라면 밑이 2인 로그를 취했을 때,
K만큼 반복해야 크기가 1인 배열로 분할 가능하다는 추론이 가능하겠죠.
그래서 분할 연산에서 logN의 시간복잡도를 소용하게 됩니다.
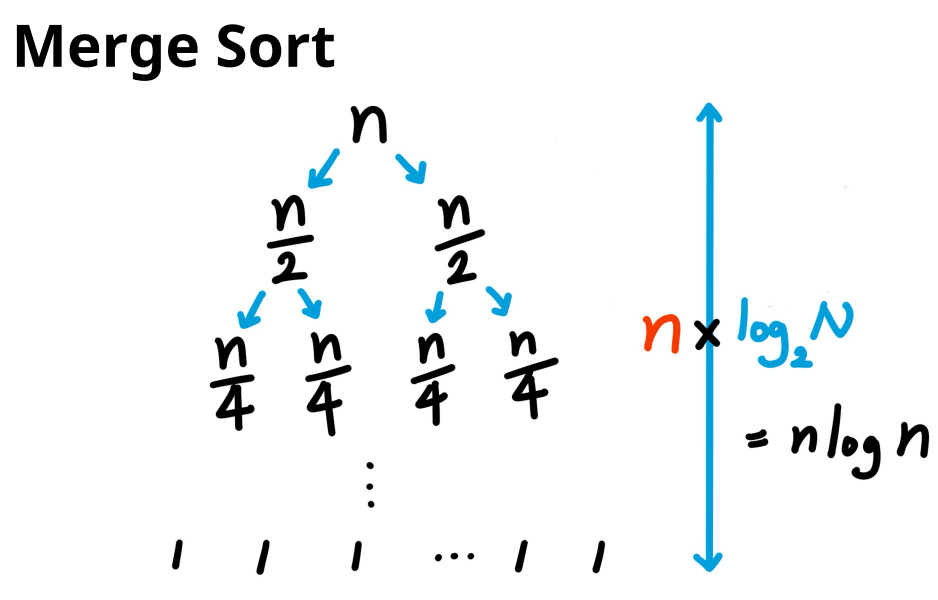
그리고 분할이 된 상태에서 다시 배열을 합칠 때
각 요소(element)들을 비교하면서 정렬을 하기 때문에 비교 연산이 수행되어야 합니다.
이 비교 연산도 시간복잡도에 포함이 됩니다.
그래서 리스트의 크기가 1인 상태일 때 크기가 1인 배열이 총 N개가 있게 되겠죠.
이 N개의 크기를 비교하면서 두개씩 합쳐진 상태의 리스트를 만들것이기 때문에 N번의 비교연산이 발생하게 됩니다.
그리고 n/4크기의 배열이 4개인 분할 상태에서도 n/4크기의 서브리스트 4개의 개수만큼 비교연산을 또 수행합니다.
결국 마찬가지로 N번의 비교연산이 발생한다는 의미입니다.
그리고 서브리스트의 크기가 n/2개일 때도
서브리스트의 개수는 총 2개고 이것을 다시 크기가 n인 배열 하나로 합칠거에요.
결국 각 뎁스(depth)에서 n개의 요소(element)만큼 크기 비교 연산을 수행하게 됩니다.
그래서 분할연산을 할 때 총 뎁스(depth)가 logN이라는 값을 구할 수 있었고,
합쳐질 때는 각 뎁스마다 비교 연산을 N번 수행하면서 합쳐지기 때문에
합병정렬(Merge sort)의 시간복잡도는 O(NlogN)이 됩니다.
로스윗의 코딩캠프는
미래의 개발자 여러분을 응원합니다.
모두 화이팅!!
알고리즘 삽입정렬(Insertion sort) 그림으로 쉽게 이해하기
알고리즘 삽입정렬(Insertion sort) 그림으로 쉽게 이해하기
알고리즘 삽입정렬(Insertion sort) 그림으로 쉽게 이해하기 안녕하세요. 로스윗의 코딩캠프입니다. 오늘은 알고리즘 정렬 중에서 삽입정렬(Insertion sort)에 대한 포스팅을 진행하겠습니다. 정말 어렵
rosweet-ai.tistory.com
알고리즘 이진탐색(Binary Search) 그림으로 쉽게 이해하기
알고리즘 이진탐색(Binary Search) 그림으로 쉽게 이해하기
알고리즘 이진탐색(Binary Search) 그림으로 쉽게 이해하기 안녕하세요. 로스윗의 코딩캠프입니다. 오늘은 정렬 알고리즘 중에서 이진탐색(Binary Search)에 대한 포스팅을 진행하겠습니다. 정말 어렵
rosweet-ai.tistory.com
'컴퓨터 공학 > 자료구조와 알고리즘' 카테고리의 다른 글
| 자료구조 트리(Tree) 그림으로 쉽게 이해하기 (0) | 2022.11.21 |
|---|---|
| 알고리즘 퀵정렬(Quick sort) 그림으로 쉽게 이해하기 (0) | 2022.11.16 |
| 알고리즘 삽입정렬(Insertion sort) 그림으로 쉽게 이해하기 (0) | 2022.11.11 |
| 알고리즘 버블정렬(Bubble sort) 그림으로 쉽게 이해하기 (0) | 2022.11.07 |
| 알고리즘 이진탐색(Binary Search) 그림으로 쉽게 이해하기 (0) | 2022.11.03 |



