그림으로 쉽게 이해하는 빅오표기법 시간복잡도
안녕하세요.
로스윗의 코딩캠프에 오신 것을 환영합니다.
오늘은 지난 시간에 이어 코딩 필수 개념인 시간복잡도에 대해서 알아보겠습니다.
거두절미 하고 바로 레츠고~!

- 시간복잡도란 무엇인가?
--> 알고리즘이 문제를 해결하기 위한 시간(연산)의 횟수를 말합니다.
먼저 가장 짧은 시간이 걸리는 O(1)부터 설명을 드리자면은,
입력 데이터의 크기와 상관없이 항상 일정한 시간이 걸리는 알고리즘을 의미합니다.
배열을 배우셨을 때 기억하실지 모르겠지만
배열에 접근할 때는 Random Access로 접근한다는 것을 아마 배우셨을 겁니다.
이렇게 접근을 하게 되면 어느 위치에 접근을 하던지간에 항상 동일한 시간에 접근 하는 것이 가능해집니다.
그래서 이 배열에 접근 할때 O(1)의 시간 복잡도를 갖는다는 것을 알수 있습니다.

- O(N)의 시간복잡도
그 다음으로 O(N)의 시간복잡도를 보겠습니다.
이것은 입력데이터의 크기에 비례해서 시간이 소요되는 알고리즘을 말합니다.
이것은 멀리갈 필요도 없이
여러분이 잘 아는 for문이 대표적인 O(N)의 시간복잡도를 갖는다고 보시면 되요.
예를들면 이 for문에서 n이 10이 되면 10번을 순회하게 되고
100이 되면 100번, n개가 되면 n번의 순회를 하기 때문에
O(N)의 시간복잡도를 갖는 것을 알 수 있습니다.

- O(N제곱)의 시간복잡도
그 다음으로 O(N제곱)의 시간복잡도를 보겠습니다.
이것은 입력 데이터의 제곱에 비례해서 시간이 소요되는 알고리즘입니다.
이것은 이중for문인경우 O(N제곱)의 시간복잡도를 갖는다고 보시면 되요.
첫번째 for문에서 N번 순회를 하고, 두번째 for문에서도 N번 순회를 하니까요.

- O(logN)의 시간복잡도
그 다음은 O(logN)의 시간복잡도를 보겠습니다.
이게 조금 어려울 수 있습니다.
이진탐색(Binary search)이라고 들어보셨나요?
쉽게 생각해서 업 다운 게임이라고 생각 하시면 되요.
1부터 100가지의 숫자가 있고, 제가 생각한 숫자를 여러분이 맞춰야 할 때
가장 효율적으로 제가 생각한 숫자를 찾을 수 있는 방법이 뭘까요?
물론 아무 값이나 불러서 때려 맞추는 것도 있겠지만
숫자를 절반씩 잘라나가면서 그 범위를 좁혀나가는 것이 가장 효율적인 방법이겠죠.
그래서 1부터 100가지의 숫자 중에서 절반인 50을 기준으로
그것보다 크면은 오른쪽 부분인 50부터 100 사이를 보면 되고
절반보다 작으면 1부터 49까지 다시 범위를 반씩 좁혀 나가면 되겠죠.
그래서 그림처럼 정렬된 숫자가 있고 9라는 숫자를 찾고 싶을 때
제일 앞에서 부터 하나씩 순회를 하면서 찾아오는 방법도 있겠지만
그럴 경우에는 한 번, 두번, 세번, 네번, 다섯번, 여섯번, 총 6번 비교 연산을 하게 되겠죠.
아래 그림을 다시 보겠습니다.
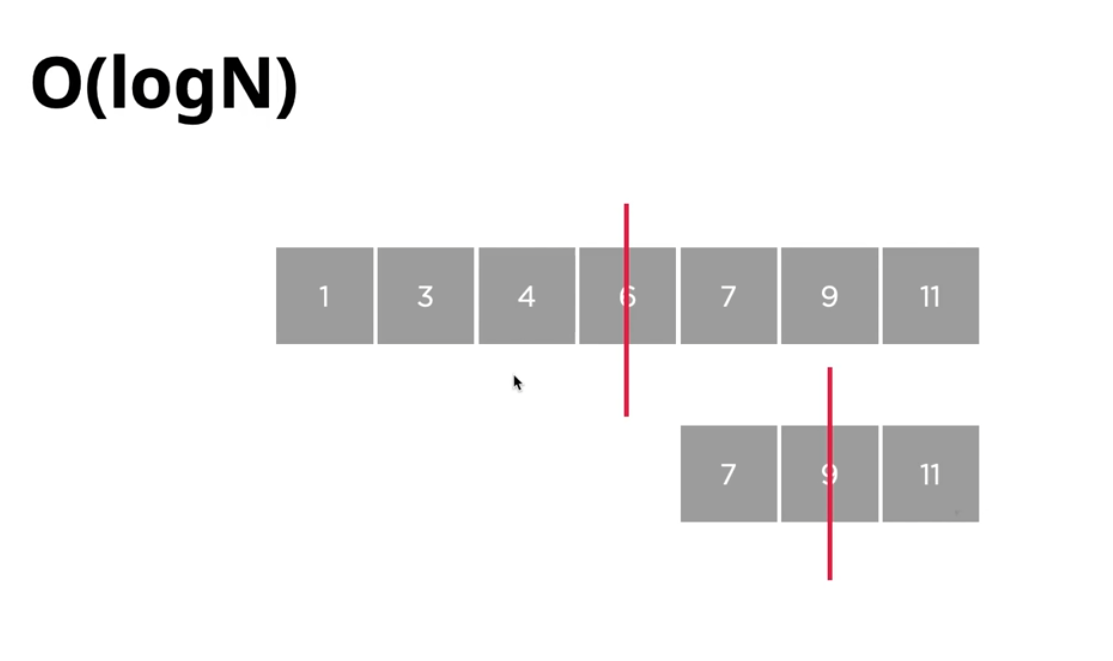
이진탐색을 통해서 9를 찾으려고 한다면
주어진 정렬된 데이터에서 중간에 위치한 값을 먼저 가져오게 됩니다.
여기서는 중앙에 위치한 6을 가져와서 비교를 해봅니다.
우리가 찾고자 하는 9는 6보다 크니까 중앙을 기준으로 오른쪽에 있는 값을 다시 살펴보게 되는거죠.
만약에 이 중간값보다 작으면 왼쪽을 보면 되겠죠.
지금의 경우는 중간값보다 크니까 오른쪽에 있는 값에서 또 다시 중앙값을 가져오게 됩니다.
이때 가져오게 되는 중앙 값은 9로 바로 우리가 찾으려고 하는 값이기 때문에
이 경우 두번의 비교 연산만으로 값을 찾아냈다고 볼 수 있겠죠.
앞에서 설명 드린 것처럼 처음부터
스캔을 하는 경우는 O(N)의 시간복잡도를 가진다고 볼 수 있습니다.
왜냐하면 데이터가 5개면 5번 10개면 10번 데이터가 n개면 n번만큼의 순회를 하기 때문에 O(N)이 되는거구요
우리가 방금 살펴본 이진탐색 binary search가 바로 O(logN) 연산이라고 보시면 됩니다.
정리하자면, 한번의 연산을 할 때마다 연산의 범위가 반 씩 줄어드는 경우에
이 logN의 시간복잡도를 가진다고 보시면 됩니다.
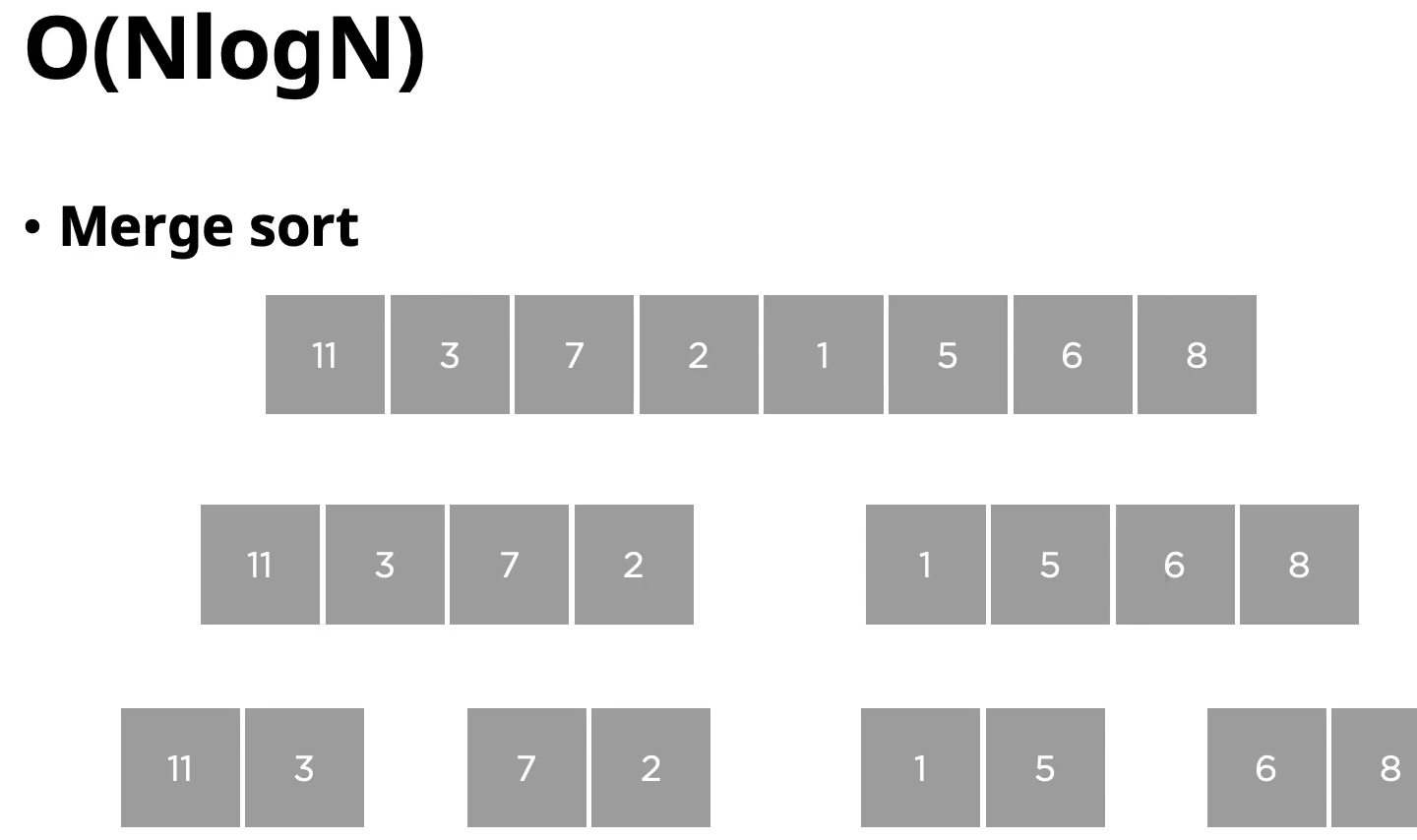
- O(NlogN)의 시간복잡도
마지막으로 O(NlogN)의 시간복잡도를 보겠습니다.
NlogN은 뒤에서 배우게 될 merge sort가 대표적인 예입니다.
정렬을 할 때 여러가지 방법이 있습니다. Quick sort도 있고, bubble sort도 있고..
그 중에 merge sort라는 방법은
주어진 데이터 집합에서 절반씩 나누면서 데이터들을 분할하는 과정을 먼저 거치게 됩니다.
이때 절반씩 나누기 때문에 앞에서 배운거처럼 logN의 시간복잡도를 먼저 가지게 됩니다.
절반씩 나눈 다음에 하나씩 값을 비교를 해가면서 다시 정렬을 하는 과정을 거치게 되는데,
이때 데이터 개수인 n번만큼 값을 비교를 하는 과정을 또 거치게 됩니다.
그래서 NlogN이라는 시간 복잡도가 나오게 됩니다.
이거는 지금 이해하기는 조금 어려운게 맞습니다.
merge sort라는 개념이 익숙하지 않고 모르는게 맞기 때문에
뒤에 가서 다시 한 번 설명을 드릴거니 걱정하지 않으셔도 되구요.
지금은 'NlogN의 시간복잡도가 있고 Merge sort라는게 있다'
라는 정도만 이해하고 넘어가도 괜찮습니다.
시간복잡도는 여기서 마무리하고
다음 포스팅부터는 본격적으로 list부터 자료구조를 공부해보도록 하겠습니다.
긴 글 읽어주셔서 감사합니다.
미래의 개발자 여러분을 코딩캠프가 응원합니다.
모두 화이팅!
개발자 여러분, 빅오표기법이 헷갈리신가요? 확실하게 알려드리겠습니다!
개발자 여러분, 빅오표기법이 헷갈리신가요? 확실하게 알려드리겠습니다!
개발자 여러분, 빅오표기법이 헷갈리신가요? 확실하게 알려드리겠습니다! 안녕하세요 로스윗의 코딩캠프입니다. 오늘도 멋진 개발자가 되기 위해 여기까지 오신 여러분을 응원합니다. 오늘은
rosweet-ai.tistory.com
Arraylist(어레이리스트) 핵중요한 특징 3가지!!
Arraylist(어레이리스트) 핵중요한 특징 3가지!!
Arraylist(어레이리스트) 핵중요한 특징 3가지!! 안녕하세요. 로스윗의 코딩캠프입니다. 오늘부터는 지난 시간에서 말씀드린대로 본격적으로 자료구조 포스팅을 시작하겠습니다. 가장 쉽고 만만한
rosweet-ai.tistory.com
'컴퓨터 공학 > 자료구조와 알고리즘' 카테고리의 다른 글
| 링크드리스트(LinkedList)의 개념과 연산 (ft. 장단점까지) (0) | 2022.10.15 |
|---|---|
| Arraylist(어레이리스트) 핵중요한 특징 3가지!! (0) | 2022.10.14 |
| 개발자 여러분, 빅오표기법이 헷갈리신가요? 확실하게 알려드리겠습니다! (2) | 2022.10.10 |
| 그림으로 쉽게 이해하는 자료구조와 알고리즘 차이 #2 (0) | 2022.10.09 |
| 그림으로 쉽게 이해하는 자료구조와 알고리즘 차이 (1) | 2022.10.08 |



